competitive programming: how to read problem statement

Basic rules

• The result of reading the statement is usually pure math model. If story helps to build correct understanding, you can keep it, but still try to discard as many unnecessary details as possible.
• Imagine you want to tell the problem to someone else. What parts you want to tell? (According to my PM, this rule won't help you).
• Shorter = better.
• Simpler = better.
• Limitations are part of problem statement. Especially small limitations, because for small data you can try all the possibilities.
• Samples are part of problem statement. After building math model, check that you model working correct on samples, at least on small samples where you can check everything fast.
• Notes are part of problem statement.
• Try to find familiar patterns, maybe objects you already know something about. If you are given some connected graph with exactly one simple path between each pair of vertices, it's called tree. 4 letters instead of 12 words, see?
• Try even harder to spot something strange, something you not expecting. That probably will be the cornerstone of the problem.
• If there is some part of the statement you don't like, try to change that to something you like. Start with understanding the object, then simplify it. There are some problems which can be completely solved by this technique.
• If the model you get is very big, try to split it into some pieces. It would be great if pieces are independent, like 'solve problem1, then use its answer as input to problem2 and so on'.
• On first stages it can be useful to write your new statement. On paper. By hand.
• Problemsetters do not write random things in statements. But why would you believe me, since I'm a bad problemsetter? I don't know, maybe you shouldn't.

Some examples

Assumed workflow: read the statement, try to understand and simplify it using the rules above. You don't have to read "solution" parts, but I warn you that my concept of reading statements works. I mean, "statement" parts will often contain huge hints to solution.
In most cases I won't write step-by-step explanations how I get the final version. You can say that that's not how teaching works. I can say that you don't want to study. I'll win, because that's my blog.

Statement

Given undirected graph, find its spanning tree with minimal diameter.

Solution

Diameter has exactly one center. Let's fix the center, it's either vertex or middle of edge. For fixed center the tree with minimal diameter is a tree with minimal height if it's rooted at center. Run BFS to find it.

Statement

We have a minimal spanning tree on Euclidian plane, we should choose its DFS order to minimize sum of distances between neighboring points. Cool, sounds like we understand the statement, what's next? Not so fast.
Let's deal with small details first. What do we mean by 'choosing DFS order'? Isn't it fixed for tree? Well, no, because we can change the order of sons for every vertex. Distances in objective function measured on plane, not on tree.
We have a minimal spanning tree on Eucl... Wait. We don't have 'a tree', we have a minimal spanning tree. Minimal spanning tree of what? Well, of complete graph on these points. OK, cool, why do we need it? Isn't problem the same for all trees? Looks like it is true. And isn't it true that any tree can be spanning for some graph? For example, let's build a graph in which weight of an edge is a distance on tree between its endpoints. For sure our tree will be MST for this graph. What a stupid person wrote this statement!
Problemsetters. DO NOT. Write. Random things.
Strange things. ARE. Important.
Let's THINK. I know, I know, it is hard, and you already showed that problemsetter is stupid, it is time to write your almighty clarification to show who is boss. But for one second. Let's analyze all the things in this statement.
Yes, it is true that any tree can be MST for some graph. But can any graph be a graph with Euclidian metric? Not really. We should have triangle inequality... and we have it for our example. So problemsetter is still stupid? Not so fast. Euclidian plane is not just a metric, it is some fixed metric. And we have geometry. We can measure angles, for example.
Let's look at our MST. Take some vertex v and two its different neighbors u and w. What do we know? The distance between u and w should be the largest among these three vertices, otherwise it won't be MST. A greater angle of a triangle is opposite a greater side. Yeah, that useless theorem from school geometry. It says that angle between two edges from one vertex is at least π / 3. And strictly greater, if vertices are in integer points. From this we can conclude that degree of any vertex in our MST is not greater than 5.
That can't be true. For sure problemsetter would write this in statement if it was true. It is limitation on input, problemsetters are obliged to write these! Oh really.
Probably there is more that you can extract from MST in Euclidian metric, but the fact about degrees is sufficient to solve a problem.

Different math models will lead you to different solutions

Well, only if you have some patterns of how you should solve problems. And you should have them, patterns are good, they're the fastest way to solve problems.

Let's think about covering given point of big circle. What small circle will cover it? Of course the closest. So, we are interested in maximal distance between some point inside big circle and closest in given set of points. That's obviously a problem on Voronoi diagram. Now O(n³) is very easy, is standard and is possible, probably only with library code :)

This observation costs medals for some teams on ICPC WF 2018. Our team also stuck with first model and didn't even try to code because implementation seems very heavy and we were sure that it will get TL. To be frank, also no one in our team could write Voronoi in , so it is not that important :)

Eliminating things you don't like can solve the problem

Given a tree, all vertices are initially white. Two players, Red and Blue, take turns coloring white vertices (surprise) red and blue. The game ends when there are no white vertices left. The score of the game is C_R - C_B, where C_R is a number of connected components on red vertices, and C_B is a number of connected components on blue vertices. Red wants to maximize the score, Blue wants to minimize it. Find the score if both play optimally. n ≤ 2·10⁵.

Solution

The statement is clear, but we don't like the formula. Especially we don't like C_i, because they change unpredictably. What can we say about connected components after deleting some vertices of a tree? Well, they are all trees themself. What we know about trees? Number of vertices is exactly 1 bigger than number of edges. OK, so number of components in a forest is exactly number of vertices minus number of edges. We can now rewrite the formula. C_R - C_B = (V_R - E_R) - (V_B - E_B) = E_B - E_R + (V_R - V_B). Value in brackets is constant, it is . So now we play not for components, but for edges. Better, but still not obvious.
We control vertices, can we somehow express E_i using only vertices? Do we have any equations expressing number of edges through vertices? Yes, we have. . But for calculating E_R we should sum only deg_R(v), the number of red neighbors. That's bad, but let's try anyways.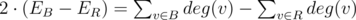
. Turns out this is true, because all RB-edges cancel out.
So, formula for score is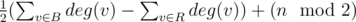
Now it is easy to see that each player should take vertex with smallest degree available at the moment.