file rename : removing non-ascii characters from filename in linux

this application for removing special characters for windows

detox -r -v /path/to/your/files


-r Recurse into subdirectories
-v Be verbose about which files are being renamed 
-n Can be used for a dry run (only show what would be changed)

competitive programming: how to read problem statement

Basic rules

• The result of reading the statement is usually pure math model. If story helps to build correct understanding, you can keep it, but still try to discard as many unnecessary details as possible.
• Imagine you want to tell the problem to someone else. What parts you want to tell? (According to my PM, this rule won't help you).
• Shorter = better.
• Simpler = better.
• Limitations are part of problem statement. Especially small limitations, because for small data you can try all the possibilities.
• Samples are part of problem statement. After building math model, check that you model working correct on samples, at least on small samples where you can check everything fast.
• Notes are part of problem statement.
• Try to find familiar patterns, maybe objects you already know something about. If you are given some connected graph with exactly one simple path between each pair of vertices, it's called tree. 4 letters instead of 12 words, see?
• Try even harder to spot something strange, something you not expecting. That probably will be the cornerstone of the problem.
• If there is some part of the statement you don't like, try to change that to something you like. Start with understanding the object, then simplify it. There are some problems which can be completely solved by this technique.
• If the model you get is very big, try to split it into some pieces. It would be great if pieces are independent, like 'solve problem1, then use its answer as input to problem2 and so on'.
• On first stages it can be useful to write your new statement. On paper. By hand.
• Problemsetters do not write random things in statements. But why would you believe me, since I'm a bad problemsetter? I don't know, maybe you shouldn't.

Some examples

Assumed workflow: read the statement, try to understand and simplify it using the rules above. You don't have to read "solution" parts, but I warn you that my concept of reading statements works. I mean, "statement" parts will often contain huge hints to solution.
In most cases I won't write step-by-step explanations how I get the final version. You can say that that's not how teaching works. I can say that you don't want to study. I'll win, because that's my blog.

Statement

Given undirected graph, find its spanning tree with minimal diameter.

Solution

Diameter has exactly one center. Let's fix the center, it's either vertex or middle of edge. For fixed center the tree with minimal diameter is a tree with minimal height if it's rooted at center. Run BFS to find it.

Statement

We have a minimal spanning tree on Euclidian plane, we should choose its DFS order to minimize sum of distances between neighboring points. Cool, sounds like we understand the statement, what's next? Not so fast.
Let's deal with small details first. What do we mean by 'choosing DFS order'? Isn't it fixed for tree? Well, no, because we can change the order of sons for every vertex. Distances in objective function measured on plane, not on tree.
We have a minimal spanning tree on Eucl... Wait. We don't have 'a tree', we have a minimal spanning tree. Minimal spanning tree of what? Well, of complete graph on these points. OK, cool, why do we need it? Isn't problem the same for all trees? Looks like it is true. And isn't it true that any tree can be spanning for some graph? For example, let's build a graph in which weight of an edge is a distance on tree between its endpoints. For sure our tree will be MST for this graph. What a stupid person wrote this statement!
Problemsetters. DO NOT. Write. Random things.
Strange things. ARE. Important.
Let's THINK. I know, I know, it is hard, and you already showed that problemsetter is stupid, it is time to write your almighty clarification to show who is boss. But for one second. Let's analyze all the things in this statement.
Yes, it is true that any tree can be MST for some graph. But can any graph be a graph with Euclidian metric? Not really. We should have triangle inequality... and we have it for our example. So problemsetter is still stupid? Not so fast. Euclidian plane is not just a metric, it is some fixed metric. And we have geometry. We can measure angles, for example.
Let's look at our MST. Take some vertex v and two its different neighbors u and w. What do we know? The distance between u and w should be the largest among these three vertices, otherwise it won't be MST. A greater angle of a triangle is opposite a greater side. Yeah, that useless theorem from school geometry. It says that angle between two edges from one vertex is at least π / 3. And strictly greater, if vertices are in integer points. From this we can conclude that degree of any vertex in our MST is not greater than 5.
That can't be true. For sure problemsetter would write this in statement if it was true. It is limitation on input, problemsetters are obliged to write these! Oh really.
Probably there is more that you can extract from MST in Euclidian metric, but the fact about degrees is sufficient to solve a problem.

Different math models will lead you to different solutions

Well, only if you have some patterns of how you should solve problems. And you should have them, patterns are good, they're the fastest way to solve problems.

Let's think about covering given point of big circle. What small circle will cover it? Of course the closest. So, we are interested in maximal distance between some point inside big circle and closest in given set of points. That's obviously a problem on Voronoi diagram. Now O(n³) is very easy, 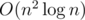is standard and is possible, probably only with library code :)

This observation costs medals for some teams on ICPC WF 2018. Our team also stuck with first model and didn't even try to code because implementation seems very heavy and we were sure that it will get TL. To be frank, also no one in our team could write Voronoi in 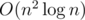, so it is not that important :)

Eliminating things you don't like can solve the problem

Given a tree, all vertices are initially white. Two players, Red and Blue, take turns coloring white vertices (surprise) red and blue. The game ends when there are no white vertices left. The score of the game is C_R - C_B, where C_R is a number of connected components on red vertices, and C_B is a number of connected components on blue vertices. Red wants to maximize the score, Blue wants to minimize it. Find the score if both play optimally. n ≤ 2·10⁵.

Solution

The statement is clear, but we don't like the formula. Especially we don't like C_i, because they change unpredictably. What can we say about connected components after deleting some vertices of a tree? Well, they are all trees themself. What we know about trees? Number of vertices is exactly 1 bigger than number of edges. OK, so number of components in a forest is exactly number of vertices minus number of edges. We can now rewrite the formula. C_R - C_B = (V_R - E_R) - (V_B - E_B) = E_B - E_R + (V_R - V_B). Value in brackets is constant, it is . So now we play not for components, but for edges. Better, but still not obvious.
We control vertices, can we somehow express E_i using only vertices? Do we have any equations expressing number of edges through vertices? Yes, we have. . But for calculating E_R we should sum only deg_R(v), the number of red neighbors. That's bad, but let's try anyways.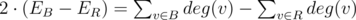
. Turns out this is true, because all RB-edges cancel out.
So, formula for score is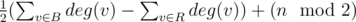
Now it is easy to see that each player should take vertex with smallest degree available at the moment.

algorithm solving steps

• REMEMBER READ THE PROBLEM STATEMENT AND DON'T SOLVE A DIFFERENT PROBLEM
• REMEMBER LOOK FOR RANDOM UNINTUITIVE DETAILS IN THE PROBLEM
• read the bounds for edge cases
• function calls are not free
• unordered naive is faster than lb vector standard

Steps:

1. Clarify Questions
2. High-level solution
3. write out steps of your solution / pseudocode
4. put some input and check if it works
5. put input in here

Framework for solving DP problems:

1. Define the objective function
2. Identify base cases
3. Write down recurrence relation ( or transiotion function) for the optimized objective function
4. What is the order of execution ? (top to buttom or buttom to top)
5. Where to look for the answer

competitive programming topics

Topic List

Category: Basics

Category: Basics

Title	Resources
Basic Topics	1 2 3

Category: Math

Category: Math

#	Title	Resources	Problems	Template	Difficulty
1	Matrix Exponentiation	1	1	code	1
2	FFT	1	1	code	2
3	NTT	1	1	code code	2
4	Online NTT	1	1 2	code	3
5	FWHT	1	1	code	2
6	Lagrange Interpolation	1	1 2	code	2
7	Lagrange Interpolation with Polynomial Extraction		1	code	3
8	Polynomial Sum	1	1	code	3
9	Polynomial with Binomial Coefficients	1	1	code	3
10	Subset Sum Problem		1 2	code	3
11	Generating Functions	1 2			3
12	Polynomial Structure	1	1	code	3
13	Polynomial Factorization of (x^n - 1)	1	1	code	3
14	Berlekamp Messey	1	1	code	3
15	Reeds–Sloane Algorithm		1	code	3
16	Linear Recurrence using Cayley-Hamilton theorem	1		code	2
17	Linear Recurrence using Generating Functions	1	1	code	3
18	Linear Recurrence with Polynomial Coefficients	1		code	3
19	Linear Recurrence on Matrices	1	1		3
20	Generating Function of a Linear Recurrence		1	code	2
21	Gaussian Elimination	1	1	code	2
22	Gaussian Elimination under Modulo	1	1	code	2
23	Gaussian Elimination Modulo 2	1	1 2	code	2
24	Determinant under Prime Modulo	1	1	code	2
25	Determinant under Composite Modulo		1	code	2
26	Determinant of Product Matrix		1	code	3
27	Determinant of Sparse Matrix		1	code	3
28	Determinant of Permutant Matrix		1	code	3
29	Determinant of Cyclic Matrix		1	code	3
30	Cauchy–Binet formula	1	1		3
31	Thomas Algorithm		1	code	2
32	Inverse of a Matrix			code	3
33	Inverse of a Matrix modulo 2		1	code	3
34	Basis Vector	1	1	code	2
35	Basis Vector Reduced Row Echelon Form.	1	1	code	2
36	Basis Vector ft Weighted Linearly Independent Vectors.		1	code	2
37	Permanent of a Matrix	1		code	2
38	All Possible Perfect Matching XOR Values		1	code	2
39	Hafnian of a Matrix	1	1	code	3
40	Vandermonde Matrix	1	1	code	3
41	Freivalds Algorithm	1		code	3
42	Characteristic Polynomial Faster / Hesserberg Matrix	1	1	code	3
43	Faulhaber's Formula Fastest	1	1	code	3
44	Lagrange Multiplier	1	1 2	code	3
45	Titu's Lemma	1 2	1 2		2
46	Simplex Algorithm	1	1	code	3
47	Integration		1	code code	2
48	Line Integral	1 2			2
49	The Slime Trick	1	1 2		3
50	Gauss's Eureka Theorem	1	1		2
51	LTE Lemma	1	1		2
52	Expected Value	1			1
53	Expected Value Powers Technique	1			2
54	Finite Field Arithmetic Binary	1	1	code	2
55	Max Convolution between Convex Funtions			code	2

Category: Number Theory

Category: Number Theory

#	Title	Resources	Problems	Template	Difficulty
56	Binary Exponentiation	1	1		1
57	Modular Inverse	1	1		1
58	Sieve	1	1	code	1
59	Sieve upto 1e9		1	code	3
60	Extended Euclid	1		code	1
61	Combinatorics Basics	1		code	1
62	Lucas Theorem	1		code	1
63	nCr Modulo Any Mod	1 2	1	code	2
64	Prefix Sum Queries of nCi		1 2	code	2
65	Sum of nCi over a Fixed Congruence Class		1	code	2
66	"Sum of nCr(a(i) k) for each k from 1 to n"		1 2	code	2
67	Sum of nCi for a Fixed Large n	1		code	3
68	Phi Function	1		code	1
69	Power Tower	1	1 2	code	2
70	Mobius Function	1	1	code	1
71	CRT	1	1 2 3 4	code	1
72	Linear Congruence Equation	1		code	1
73	Pollard Rho	1	1	code	2
74	Primitive Root	1	1	code	2
75	Multiplicative Order / Carmichael's Lambda Function	1	1	code	2
76	Discrete Log	1	1 2	code	2
77	Discrete Root	1	1	code	2
78	Discrete Root in O(p^(1/4)) using Tonelli-Shanks Algorithm	1	1	code	3
79	Number of Distinct Kth Powers Modulo n	1		code	3
80	Number of Solutions to x^2 = 1 mod m	1	1	code	2
81	Tonelli Shanks Algorithm	1	1 2	code	3
82	Pells Equation	1 2	1	code	3
83	Linear Diophantine Equation with Two Variables	1	1	code	1
84	Trivariable Linear Diophantine Equation with Nonnegative Solutions	1	1	code	3
85	Multivariable Linear Diophantine Equation with Nonnegative Solutions	1	1 2	code	3
86	Linear Diophantine With N Unknowns and Two Equations		1	code	3
87	Floor Sum of Arithmetic Progression	1	1 2	code	2
88	Generalized Floor Sum of Arithmetic Progression	1	1	code	3
89	Sum of Floors			code	1
90	Number of Nonnegative Integer Solutions to ax+by ≤ c			code	3
91	Number of ax % p in a Range			code	3
92	Smallest Nonnegative Integer x s.t. l ≤ ax % p ≤ r		1 2	code	3
93	Prime Counting Function	1	1 2	code	2
94	K Divisors		1 2	code	3
95	Smallest Number Having Exactly K Divisors		1	code	2
96	Sum of The Number of Divisors in cbrt(n)		1	code	3
97	Linear Sieve for Multiplicative Functions	1		code	1
98	Min_25 Sieve	1 2 3	1 2	code	3
99	Mobius Inversion	1	1 2		2
100	Dirichlet convolution	1 2	1 2 3	code	2
101	Number of Solutions to a Basic Linear Algebraic Equation	1	1	code	1
102	Number of Solutions to a Basic Linear Algebraic Equation with Variable Upper Bound Constraints	1	1 2 3	code	3
103	Partition Function	1	1	code	3
104	Stirling Number of the First Kind for Fixed n	1	1	code	2
105	Stirling Number of the First Kind for Fixed k	1		code	3
106	Stirling Number of the Second Kind for Fixed n	1	1	code	2
107	Stirling Number of the Second Kind for Fixed k	1	1	code	3
108	Bell Number	1		code	2
109	LCM of Fibonacci Numbers	1	1	code	2
110	Phi Field		1 2	code	2
111	Pisano Period	1	1 2	code	3
112	Rational Approximation / Stern-Brocot Tree	1 2 3	1	code	3
113	Factoradic Number System	1	1	code	2
114	Intersection of Arithmetic Progressions	1		code	1
115	Continued Fractions	1 2	1	code	2
116	Maximum Coprime Product		1	code	2

Category: Graph Theory

Category: Graph Theory

#	Title	Resources	Problems	Template	Difficulty
117	DFS and BFS	1 2	1		1
118	0/1 BFS	1	1		1
119	Dial's algorithm	1			2
120	Inverse Graph	1	1 2	code	1
121	LCA	1	1	code	1
122	LCA in O(1)	1	1	code	2
123	SCC	1	1	code	1
124	Incremental SCC	1 2			3
125	DFS Tree	1			1
126	Rerooting Technique	1			1
127	Articulation Bridges and Bridge Tree	1 2	1 2	code	1
128	Online Articulation Bridges	1		code	3
129	Strong Orientation	1	1		1
130	Articulation Points.	1	1	code	1
131	Block Cut Tree	1	1	code	2
132	Three Edge Connectivity	1	1 2	code	3
133	Four Edge Connectivity	1			3
134	Dynamic K-Connectivity	1			3
135	Prim's MST	1	1	code	1
136	Krushkal's MST	1	1	code	1
137	Steiner Tree Problem	1	1	code	2
138	Boruvka's Algorithm	1	1	code	2
139	Minimum Diameter Spanning Tree	1	1 2	code	3
140	Manhattan MST		1	code	3
141	Euclidean MST	1			3
142	Directed MST	1	1	code	3
143	Dynamic MST	1	1	code	3
144	Dijkstra's Algorithm	1	1	code	1
145	Dijkstra on Segment Tree		1	code	2
146	Bellman Ford	1	1	code	1
147	Floyd Warshall	1	1	code	1
148	Johnsons Alogrithm	1	1	code	2
149	SPFA	1	1	code	1
150	Cycle Detection	1	1	code	1
151	Minimum Weight Cycle For Each Vertex		1	code	2
152	Minimum Weight Cycle For Each Edge		1	code	2
153	Dominator tree	1	1	code	2
154	2 SAT	1	1 2	code	1
155	3 SAT			code	3
156	Maximum Clique	1 2	1	code	1
157	Number of Different Cliques			code	2
158	Maximum Independent Set		1	code	1
159	Eulerian Path on a Directed Graph	1	1	code	1
160	Eulerian Path on an Undirected Graph	1	1	code	1
161	Path Union		1 2	code	2
162	Path Intersection		1	code	2
163	Virtual Tree	1	1 2 3	code	2
164	Welsh-Powell Algorithm	1 2			2
165	Chromatic Number	1	1	code	1
166	Chromatic Polynoimial ft Number of DAGs		1	code	3
167	Dynamic DAG Reachability	1	1	code	3
168	Minimum Mean Weight Cycle		1	code	3
169	Number of 3 and 4 length Cycles		1	code	3
170	Counting Labeled Graphs	1		code	1
171	Chordal Graph	1	1	code	2
172	Cactus Graph	1 2	1		2
173	Edge Coloring of Simple Graph		1 2	code	3
174	Edge Coloring of Bipartite Graph			code code	3
175	Dynamic Diameter Online		1	code	3
176	Tree Orientation to Maximize Pairs of Reachable Nodes	1	1	code	3
177	Number of Arborescences with n Nodes			code	2
178	Kirchoffs Theorem ft Number of MSTs	1	1	code	2
179	Tuttes Theorem ft Arborescences in a Graph	1	1	code	2
180	BEST Theorem	1			2
181	System Of Difference Constraints	1	1	code	2
182	Prufer Code	1	1	code	1
183	Number of Ways to Make a Graph Connected	1			1
184	Tree Isomorphism	1	1 2 3	code	1
185	Number of Paths of Each Length in a Tree			code	2
186	Ear Decomposition	1	1		2
187	Eppsteins Algorithm	1	1	code	3
188	Hamiltonian Path Heuristic Algorithm	1			3
189	Erdos Gallai Theorem	1			2
190	Havel Hakimi Algorithm	1 2			2
191	Dinics Algorithm	1	1	code	1
192	Push Relabel Algorithm	1		code	2
193	Min Cost Max Flow	1	1 2	code	2
194	Min Cost Max Flow with Negative Cycles			code	3
195	Maximum Closure Problem	1	1 2	code	2
196	Min Cut in a Planar Graph	1	1	code	2
197	Max Cut in a Planar Graph		1		3
198	Unique Min Cut	1	1	code	2
199	L-R Flow	1	1 2	code code	2
200	Gomory-Hu Tree	1	1	code	3
201	Gomory Hu Tree of a Planar Graph		1	code	3
202	Stoer Wagner Algorithm	1	1	code	3
203	HopCroft Karp Algorithm	1		code	1
204	Kuhns Algorithm	1	1	code	1
205	Hungarian Algorithm	1	1	code	1
206	Blossom Algorithm	1	1	code	2
207	Blossom Algorithm Weighted		1	code	3
208	Chinese Postman Problem	1	1	code	1
209	ST-numbering	1		code	3
210	POSET ft Dilworths and Mirskys Theorem	1 2	1		2
211	Stable Marriage Problem	1	1	code	2
212	Halls Theorem	1	1		1
213	Maximum Density Subgraph	1	1	code	3
214	Randomized Matching			code code	2
215	Number of Perfect Matchings in a Graph	1	1	code	3
216	Planarity Check	1 2			3

Category: Data Structures

Category: Data Structures

#	Title	Resources	Problems	Template	Difficulty
217	Segment Tree	1	1 2	code	1
218	Segment Tree with Lazy Propagation	1	1 2	code	1
219	Persistent Segment Tree	1	1	code	1
220	Persistent Segment Tree with Lazy Propagation	1	1	code	2
221	Dynamic Segment Tree	1			1
222	2D Dynamic Segment Tree		1	code	2
223	Iterative Segment Tree	1		code	1
224	Segment Tree ft Arithmetic Progressions		1	code	1
225	Segment Tree Merging	1	1	code	2
226	Segment Tree Beats	1	1	code	3
227	Merge Sort Tree	1	1		1
228	Wavelet Tree	1	1	code	1
229	Sparse Table	1	1	code	1
230	Disjoint Sparse Table	1	1	code	2
231	Sparse Table 2D	1	1	code	2
232	BIT	1	1	code	1
233	Lower bound on BIT	1	1		1
234	BIT with Range Update and Range Query	1		code	2
235	2D BIT with Range Update and Range Query			code	2
236	MOs Algorithm	1 2	1	code	1
237	MOs on Tree	1	1	code	2
238	MOs with Update	1 2	1	code	2
239	MOs Online		1	code	2
240	MOs with DSU		1 2	code	2
241	Sweepline MO	1			3
242	Trie	1	1	code	1
243	Persistent Trie	1	1	code	2
244	DSU	1	1	code	1
245	Reachability Tree/ DSU Tree	1	1 2	code	2
246	DSU with Rollbacks			code	1
247	Partially Persistent DSU	1	1	code	3
248	Persistent DSU		1	code	3
249	Augmented DSU	1		code	2
250	Queue Undo Trick	1	1 2	code	3
251	Dynamic Connectivity Problem	1	1	code	2
252	DSU on Tree	1	1	code	1
253	SQRT Decomposition	1	1		1
254	SQRT Decomposition Split and Build Technique		1	code	3
255	Centroid Decomposition	1	1		1
256	Persistent Centroid Decomposition		1	code	3
257	Binarizing a Tree		1	code	1
258	HLD ft Subtrees and Path Query	1 2	1	code	2
259	HLD ft Persistent Lazy Propagation		1	code	3
260	LCT	1	1	code	2
261	Treap	1	1	code	2
262	Implicit Treap	1	1	code	2
263	Persistent Treap		1 2	code	3
264	SQRT Tree	1	1	code	3
265	KD Tree	1	1	code	2
266	Cartesian Tree	1		code	2
267	Rope	1	1		1
268	Monotonous Queue	1	1	code	1
269	BST using STL	1		code	1
270	Persistent BST	1			3
271	Ordered Set	1 2	1	code	1
272	Static to Dynamic Trick	1 2		code	2
273	Interval Set			code	2
274	Divide and Conquer on Queries		1		2
275	Divide and Conquer for Insert and Query Problems	1	1	code	2
276	Venice Technique	1	1	code	1
277	Permutation Tree	1		code	3
278	Persistent Array		1	code	1
279	Persistent Queue		1	code	3
280	Persistent Meldable Heap	1	1	code	2
281	Top Tree	1	1	code	3
282	PQ Tree	1	1		3
283	Link Cut Cactus	1	1		3
284	HDLT	1			3

Category: Strings

Category: Strings

#	Title	Resources	Problems	Template	Difficulty
285	KMP	1	1	code	1
286	Prefix Automaton	1		code	1
287	Z algorithm	1	1	code	1
288	Aho Corasick	1	1 2	code	1
289	Dynamic Aho Corasick	1		code	2
290	Aho Corasick ft All Pair Occurrence Relation		1	code	2
291	String Matching using Bitsets		1 2	code	1
292	String Matching with FFT	1	1 2	code	2
293	String Hashing	1	1 2	code	1
294	2D String Hashing	1	1	code	2
295	Suffix Array	1	1	code	2
296	Isomorphic Suffix Array		1	code	3
297	Suffix Automaton	1	1	code	2
298	Suffix Automaton ft Distinct Substring Queries in Range.		1 2		3
299	Suffix Tree	1			3
300	Palindromic Tree	1	1	code	2
301	Persistent Palindromic Tree		1	code	3
302	Manachers Algorithm	1	1	code	2
303	Minimum Palindrome Factorization	1	1	code	3
304	Number of Palindromes in Range	1	1 2	code	2
305	Lyndon Factorization	1	1		2
306	Main-Lorentz Algorithm	1			3
307	All Substring Longest Common Subsequence	1		code	3
308	Bit LCS		1	code	3
309	Cyclic LCS			code	3
310	De Bruijn Sequence			code	1
311	LCS on RLE compressed string	1			3

Category: DP

Category: DP

#	Title	Resources	Problems	Template	Difficulty
312	Digit DP	1	1	code	1
313	CHT	1 2	1	code	2
314	Dynamic CHT	1	1	code	2
315	Persistent CHT			code	3
316	Li Chao Tree	1 2	1 2	code	2
317	Persistent Li Chao Tree		1 2	code	2
318	Extended Li Chao tree	1			3
319	Divide and Conquer Optimization	1	1	code	1
320	Knuth Optimization	1 2	1	code	1
321	Substring DP	1	1	code	1
322	Bounded Knapsack	1	1	code	1
323	SOS DP	1	1	code	1
324	Subset Sum Convolution	1		code	2
325	Dynamic Submask Count		1	code	2
326	DP over Divisors			code	1
327	Subset Sum in SQRT		1	code	1
328	LIS Range Query	1	1		2
329	Aliens Trick	1	1		2
330	1D1D DP Optimization	1	1	code	3
331	Connected Component DP	1	1	code	3
332	Slope Trick	1	1		2
333	Subset Union of Bitsets		1	code	2
334	Number of Subsequences Having Product at least K		1	code	2
335	Hirschbergs Algorithm	1	1		3
336	Broken Profile DP/plug dp	1 2	1		2
337	XOR Equation	1	1 2 3		2
338	"x2 +1 trick"	1	1	code	1
339	Open and Close Interval Trick	1	1		1
340	Bitmask DP	1	1		1

Category: Geometry

Category: Geometry

#	Title	Resources	Problems	Template	Difficulty
341	Geometry 2D Everything	1 2 3 4	1	code	3
342	Basic Point Structure(2D)	1		code	1
343	Polar Sort(2D)	1		code	1
344	Basic Line Structure(2D)	1		code	1
345	Angle Bisector(2D)	1		code	1
346	Dist from Point to Line(2D)	1		code	1
347	Dist from Point to Ray(2D)	1		code	1
348	Dist from Point to Segment(2D)	1		code	1
349	Dist from Segment to Segment(2D)	1		code	1
350	Check if Point is on Segment(2D)	1		code	1
351	Line Line Intersection(2D)	1		code	1
352	Point Line Relation(2D)	1		code	1
353	Project from Point to Line(2D)	1		code	1
354	Project from Point to Segment(2D)	1		code	1
355	Ray Ray Distance(2D)	1		code	1
356	Ray Ray Intersection(2D)	1		code	1
357	Reflection from Point to Line(2D)	1		code	1
358	Segment Line Intersection(2D)	1		code	1
359	Segment Line Relation(2D)	1		code	1
360	Segment Segment Intersection(2D)	1		code	1
361	Basic Circle Structure(2D)	1		code	1
362	Circle Circle Area(2D)	1		code	1
363	Circle Circle Intersection(2D)	1		code	1
364	Circle Circle Relation(2D)	1		code	1
365	Circle Line Intersection(2D)	1		code	1
366	Circle Line Relation(2D)	1		code	1
367	Circle Point Relation(2D)	1		code	1
368	Tangent Lines from Point(2D)	1		code	2
369	Tangent Lines from Circle(2D)	1		code	2
370	Maximum Circle Cover(2D)	1		code	2
371	Maximum Inscribed Circle(2D)	1		code	2
372	Triangle Circle Intersection(2D)	1		code	2
373	Polygon Circle Intersection(2D)	1		code	2
374	Circle Union(2D)	1		code	3
375	Centroid of a Polygon(2D)	1		code	1
376	Convex Hull(2D)	1		code	1
377	Diameter of a Convex Polygon(2D)	1		code	2
378	Extreme Vertex(2D)	1		code	2
379	Geometric Median(2D)	1		code	2
380	Convexity Check(2D)	1		code	1
381	Check if Point is in Convex(2D)	1		code	2
382	Check if Point is in Polygon(2D)	1		code	2
383	Minimum Enclosing Circle(2D)	1		code	2
384	Minimum Enclosing Rectangle(2D)	1		code	2
385	Polygon Line Intersection(2D)	1		code	2
386	Width of a Polygon(2D)	1		code	2
387	Winding Number(2D)	1		code	2
388	Dist from Point to Polygon(2D)	1		code	2
389	Dist from Polygon to Line(2D)	1		code	2
390	Dist from Polygon to Polygon(2D)	1		code	2
391	Maximum Dist from Polygon to Polygon(2D)	1		code	3
392	Tangents from Point to Polygon(2D)	1		code	3
393	Polygon Union(2D)	1		code	3
394	Minkwoski Sum(2D)	1		code	2
395	Geometry 3D Everything	1		code	3
396	Basic Point Structure(3D)	1		code	1
397	Basic Line Structure(3D)	1		code	1
398	Plane Structure(3D)	1		code	1
399	3D Coordinates to 2D	1		code	1
400	Distance from Segment to Point(3D)	1	1	code	2
401	Distance from Triangle to Point(3D)	1	1	code	2
402	Distance from Triangle to Segment(3D)	1	1	code	2
403	Distance from Triangle to Triangle(3D)	1	1	code	2
404	Distance from Segment to Segment(3D)	1			2
405	Plane Plane Intersection	1		code	2
406	Basic Sphere Structure	1		code	1
407	Sphere Line Intersection	1		code	2
408	Segment Segment Intersection on Sphere	1		code	2
409	Oriented Angle on Sphere	1		code	2
410	Area on The Surface of The Sphere	1		code	2
411	Winding Number 3D	1		code	3
412	Convex Hull 3D	1	1	code	3
413	Picks Theorem	1 2	1		1
414	Closest Pair of Points	1	1	code	1
415	All Pair Segment Intersection.	1	1	code	3
416	Dynamic Convex Hull			code	3
417	Delaunay Triangulation	1	1	code	3
418	Voronoi Diagram	1	1	code	3
419	Half Plane Intersection	1	1	code	2
420	Dynamic Half Plane Intersection		1	code	3
421	Onion Decomposition	1	1	code	3
422	Point Location	1	1	code	3
423	Convex Hull Intersection using Minkowski				2
424	Generating Points without Collinear Triplets	1			2
425	Maximum Area of a Triangle from given Lengths		1	code	3
426	Vertical decomposition	1	1		3

Category: Game Theory

Category: Game Theory

#	Title	Resources	Problems	Template	Difficulty
427	Grundy Number	1 2			1
428	Green Hackenbush on Trees and Graphs		1 2	code	2
429	Blue Red HackenBush	1	1	code	3
430	Games on Arbitrary Graphs	1			2
431	Matching Game On A Graph	1	1	code	2
432	Nimber	1			3

Category: Miscelleneous

Category: Miscelleneous

#	Title	Resources	Problems	Template	Difficulty
433	Bigint			code	2
434	Two Pointers	1			1
435	Binary Search	1			1
436	Fraction Binary Search		1	code	3
437	Ternary Search	1		code	1
438	Parallel Binary Search	1	1		2
439	Josephus Problem	1		code	1
440	Permutation with no Arithmetic Progression	1	1		1
441	Balanced Brackets	1			1
442	Knight Moves in Infinity Grid			code	2
443	Bishop Placement	1			1
444	Gray Code	1	1	code	1
445	MEX of all Subarrays		1	code	3
446	Dates			code	1
447	Schreier–Sims Algorithm	1	1	code	3
448	Expression Parsing	1		code	1
449	Randomized Algorithms	1			2
450	K-th Root of a Permutation	1	1	code	3
451	Matroid Intersection	1 2 3 4 5	1	code	3
452	SMAWK Algorithm	1			3
453	Lindstrom–Gessel–Viennot lemma	1	1		3

Category: Important Links

Category: Important Links

Title	Resources
Useful blogs	1
USACO Guide	1
Helpful Extensions	1
Stress Testing	1
Problems That Will Make You Learn Something New	1

Category: Recently Added